跳转至

Week 3

约 824 个字 142 行代码 1 张图片 预计阅读时间 5 分钟

Summary

大概需要2.5小时，Lab质量相当高，可以很好的弥补理解上的一些问题

Videos(1h)

Functional Abstraction

Lambda Function Environments

This is main case:

Python
a = 1
def f(g):
    a = 2
    return lambda y: a * g(y)
f(lambda y: a + y)(a)

# we can get 4(2 * (1 + 1))

Return

Python
def search(f):
    """找出能够返回Ture的最小非负整数"""
    x = 0
    while True:
        if f(x):
            return x
        x += 1
    # 下面是一个改进版本
    while not f(x):
        x += 1
    return x

def inverse(f):
    """Return g(y) such that g(f(x)) -> x."""
    # 找出使f(x)=y成立的最小x
    return lambda y: search(lambda x: f(x) == y)

# 找反函数
sqrt = inverse(square)

Abstraction

Choose a name for valued function or parameters.

Some name guideline.

Errors & Tracebacks

Teach you check some errors and read tracebacks

Function Examples

Midterm 1 Review

  • WWPP
Python
def delay(arg):
    print('delayed')
    def g():
        return arg
    return g

delay(delay)()(6)()

# 分析
# delay(delay) -> 返回g 传入参数为delay函数 print也被调用
# delay(delay)() -> 调用g 返回delay
# delay(delay)()(6) -> 调用delay 传入参数为6 相当于delay(6)=g print也被调用
# delay(delay)()(6)() -> 调用g() 上一步知道传入参数为6 返回6

print(delay(print)()(4))

# 同理分析即可

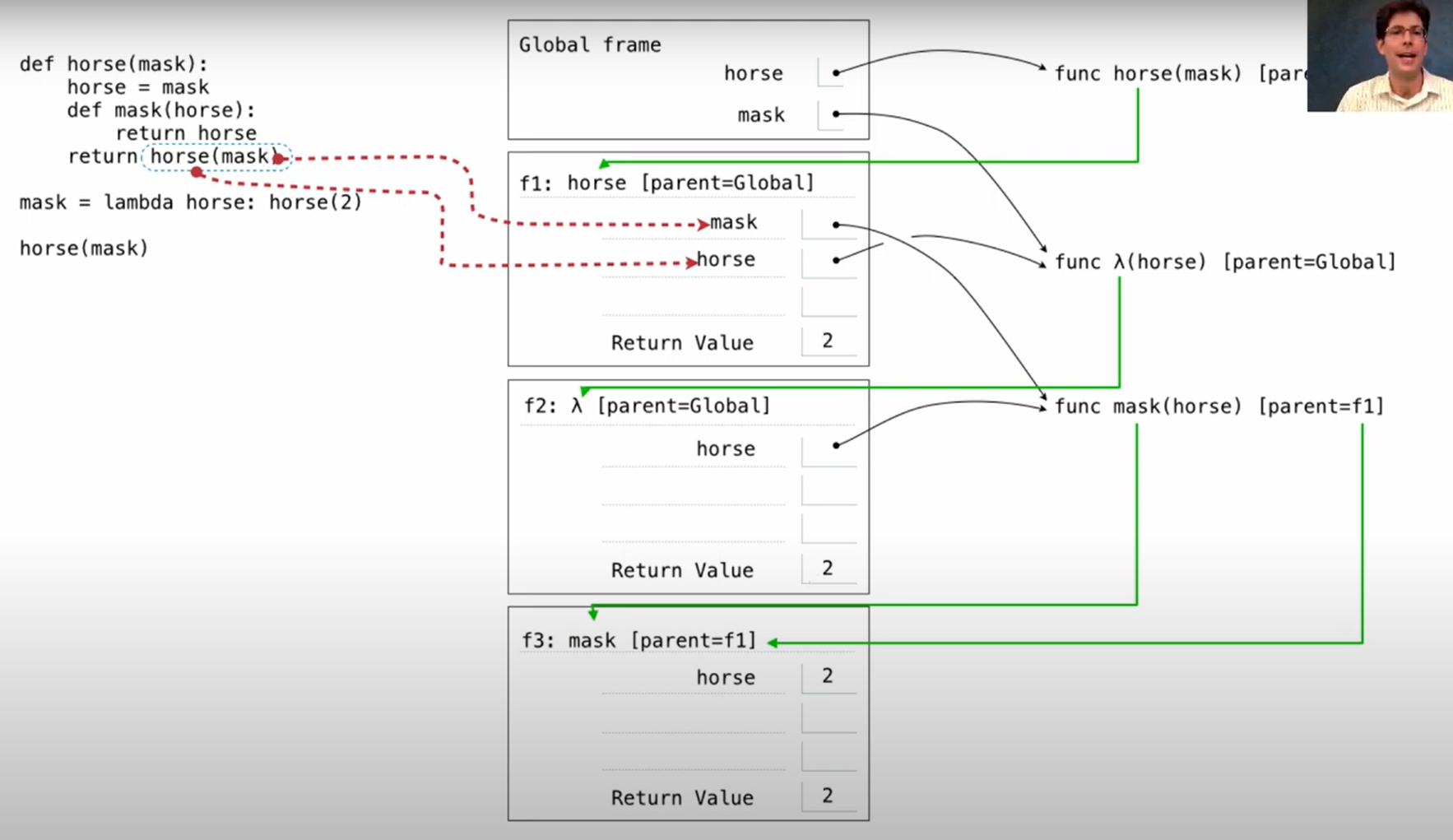
Last example but a litttle difficult

Python
def horse(mask):
    horse = mask
    def mask(horse):
        return horse
    return horse(mask)

mask = lambda horse: horse(2)

horse(mask)

有一种当年玩指针的美感(只要正确的指向就可以明白，这里的环境图确实是加进理解的一种手段)

env-horse-mask

Implementing Functions

Strategy:

  • Read the description
  • Verify the example & pick a simple one
  • If the template is helpful, use it
  • Write cide to compute the result

A case

Python
def remove(n, digit):
    kept, digits = 0, 0
    while n > 0:
        n, last = n // 10, n % 10
        if last != digit:
            kept = kept + last * 10 ** digits
            digits += 1
    return kept

Decoraters

Python
def trace1(fn):
"""Return a version of fn"""
    def traced(x):
        print('Calling', fn, 'on argument', x)
        return fn(x)
    return traced

@trace1 # square = trace1(square)
def square(x):
    return x * x

@trace1
def sum_squares_ up_to(n):
    k = 1
    total = 0
    while k <= n:
        total, k = total + square(k), k + 1
    return total

Lab 02(1h)

前面是一些基础的Review部分，算是强行带你复习吗?感觉还是不错的，给出了Short-circuiting这个概念详细的解释

这里需要注意lambda表达式和def表达式的一些细微区别

Python
# A lambda expression by itself does not alter
# the environment
lambda x: x * x
# We can assign lambda functions to a name
# with an assignment statement
square = lambda x: x * x
square(3)

# Lambda expressions can be used as an operator
# or operand
negate = lambda f, x: -f(x)
negate(lambda x: x * x, 3)

Note: As we saw in the lambda expression section above, lambda functions have no intrinsic name. When drawing lambda functions in environment diagrams, they are labeled with the name lambda or with the lowercase Greek letter λ. This can get confusing when there are multiple lambda functions in an environment diagram, so you can distinguish them by numbering them or by writing the line number on which they were defined.

WWPD

Q1: WWPD: The Truth Will Prevail

If and and or do not short-circuit, they just return the last value; another way to remember this is that and and or always return the last thing they evaluate, whether they short circuit or not. Keep in mind that and and or don't always return booleans when using values other than True and False.

Used above info.

Python
# 有点阴的例子
print(3) or ''
# print会执行但是返回的None是假值，而空字符串也是假值，于是最终返回最后计算的空字符串
# 3
# ''

只要做完就会对短路求值这件事彻底理解

Q2: WWPD: Higher-Order Functions

这个也有点搞，需要稍微仔细一点去想返回的是函数还是调用函数

Q3: WWPD: Lambda

Python
# case 无参数 还真没想过
(lambda: 3)()

注：这个lab真是大开眼界了

Coding Practice

Q4: Composite Identity Function

Q5: Count Cond

这些代码并不难，答案也没有什么很优雅的做法

Environment Diagram Practice

Q6: HOF Diagram Practice

Optional Questions

Q7: Multiple

实际上应该是找最小公倍数的问题，有很多优化算法，偷懒打个简单的

Python
i = 1  
while True:  
    if (max(a, b) * i) % min(a, b) == 0:  
        return max(a, b) * i  
    else:  
        i += 1

可能答案想打个遍历吧，但是显然这样复杂度对于大数来说不划算

Q8: I Heard You Liked Functions...

这个题目也是够套娃的...但是也还好逻辑比较简单

Define a function cycle that takes in three functions f1, f2, and f3, as arguments. cycle will return another function g that should take in an integer argument n and return another function h. That final function h should take in an argument x and cycle through applying f1, f2, and f3 to x, depending on what n was. Here's what the final function h should do to x for a few values of n:

  • n = 0, return x
  • n = 1, apply f1 to x, or return f1(x)
  • n = 2, apply f1 to x and then f2 to the result of that, or return f2(f1(x))
  • n = 3, apply f1 to x, f2 to the result of applying f1, and then f3 to the result of applying f2, or f3(f2(f1(x)))
  • n = 4, start the cycle again applying f1, then f2, then f3, then f1 again, or f1(f3(f2(f1(x))))
  • And so forth.

Hint: most of the work goes inside the most nested function.

保险起见写了一个特别简单的版本，可以参考答案的做法

Python
def classifier(n):  
    def inner_loop(x):  
        i = 1  
        while i <= n:  
            if (i % 3) == 1:  
                x = f1(x)  
            elif (i % 3) == 2:  
                x = f2(x)  
            elif (i % 3) == 0:  
                x = f3(x)  
            i += 1  
        return x  
    return inner_loop  
return classifier

优雅的递归解法

Python
def g(n):  
    def h(x):  
        if n == 0:  
            return x  
        return cycle(f2, f3, f1)(n - 1)(f1(x))  
    return h  
return g

Disc 02(30min)

相应的测试代码在CS61A的仓库内

Q1: Warm Up

trivial

Q2：Make Keeper

也是很简单的

Python
def cond(f):  
    i = 1  
    while i <= n:  
        if f(i):  
            print(i)  
        i += 1  
return cond

Q3: Digit Finder

Python
def give_digit(x):  
    return (x // (pow(10, k-1))) % 10  
return give_digit

答案使用的是lambda匿名封装(效果可能差不多但是有点帅，想学)

Python
return lambda x: (x // pow(10, k-1)) % 10

Q4: Match Maker

也比较简单，因为已给出了一个框架

Python
def check(x):  
    while x // (10 ** k) > 0:  
        if (x % 10) != (x // (10 ** k)) % 10:  
            return False  
        x //= 10  
    return True  
return check

总的来说Disc还是比较简单的

评论