Week 2¶

Summary¶

先看Videos再看Reading，需要注意的是Ch 1.6内容很多，每天的Videos只是讲解了其中的一部分内容并且有时不按顺序，可以先全部看完Videos再看Reading

大致需要6h完成(不包括project)

Videos(2h)¶

Control¶

Multiple Environments¶

Life cycle of a User-Defined Function:

• Def statement
• Call expression
• Calling/Applying

Names have no meaning without environments

Names have different meanings in different environments

Miscellaneous Python Features¶

• truediv and floordiv
• mod operator

Vim?!

doc test¶

from operator import floordiv, mod

def divide_exact(n,d):
    """Return the quotient and remainder of diving N by D.

    >>> q, r = divide_exact(2013, 10)
    >>> q
    201
    >>> r
    2
    """
    return floordiv(n, d), mod(n, d)

# We can type python3 -m doctest -v filename.py to get results 

default value (not assignment)： 只是作为一个占位符，在没有赋值的情况下使用，并不是赋值操作

Conditional statements¶

def absolute_value(x):
    """Return the absolute value of x"""
    if x < 0:
        return -x
    elif x == 0:
        return 0
    else:
        return x

George Boole: boolean contexts

Iteration¶

Iteration means repeating things

i, total = 0, 0
while i < 3:
    i = i + 1
    total = total + i

这个部分就是讲解简单的循环逻辑，感觉可以不用看.

Higher-Order Functions¶

Iteration Example¶

talk about Fibonacci sequence and quite trivial

Control¶

用一个函数来表达判断的结构

Control Expressions¶

Some expressions can be passed in Python like (left and right && or)

def has_big_sqrt(x)
    return x > 0 and sqrt(x) > 10

# 聪明的设计，这时输入-1000 程序并不会崩溃，说明右侧程序不执行

精度丢失问题：

def reasionable(n):
    return n == 0 or 1 / n != 0

>>>reasionable(10 ** 10000)
False

Higher-Order Functions¶

1.Generalizing Patterns with Arguments

• Find common shape
• share solving method

assert statement:

like assert r > 0, 'A length must be positive'

2.Generalizing Over Computational Processes

将模式抽象出来进行归纳式的解决以函数为参量，是一种很自然的想法

Functions as Return Values¶

def make_adder(n):
    def adder(k):
        return k + n # 取决于make_adder的输入
    return adder 

>>> add_three = make_adder(3)
>>> add_three(4)
7

The purpose of Higher-Order Functions

• Express general methods of computation
• Remove repetition from programs
• Separate concerns among functions

Environments¶

Environments for Higher-Order Functions¶

def apply_twice(f, x):
    return f(f(x))

def square(x)
    return x * x

result = apply_twice(square, 2)

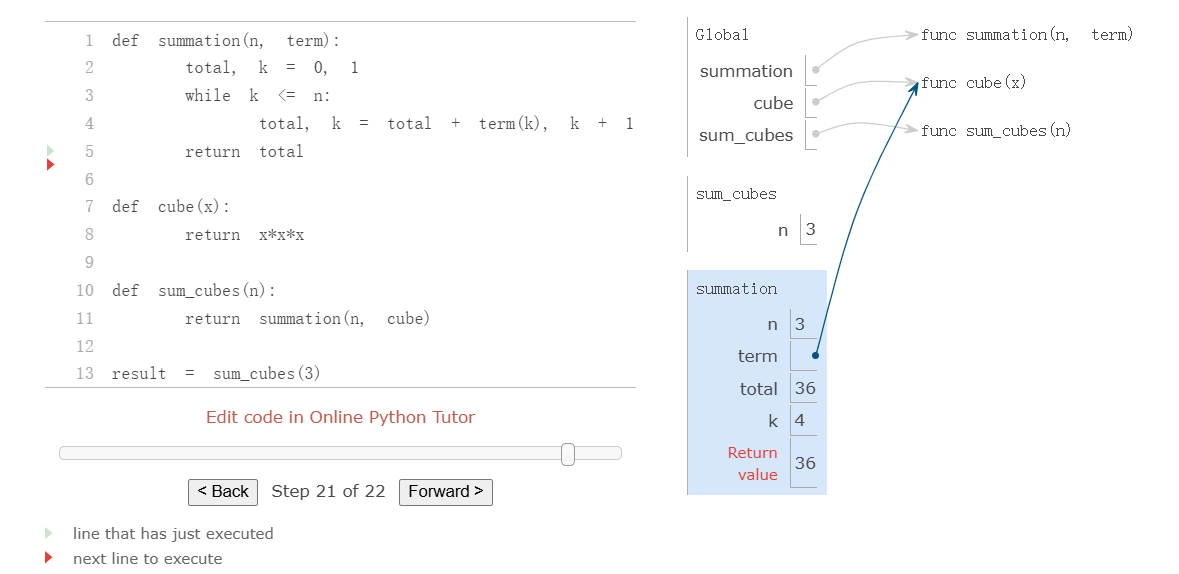
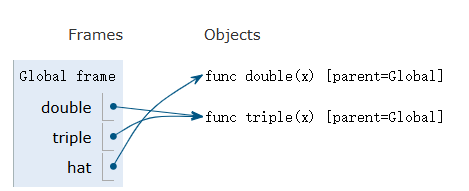
Environments for Nested Definitions¶

Mainly about how to draw environment diagram and decide the parent frame of any function.

Local names¶

Formal parameters of functions have a local scope means that if we call a function but the parameter of it doesn't be defined in local frame, it will cause an error.

Function Composition¶

Use some simple functions to compose a big function.

def compose1(f, g):
    def h(x):
        return f(g(x))
    return h

Lambda Expressions¶

由于它没有return部分，使用lambda只能创建简单的函数，在Python中也不经常用，但是对于其他语言常用(我学Python和R的，我可以不看吗？)

Only the def statement gives the function an intrinsic name.

Function Currying¶

def curry2(f):
    def g(x):
        def h(y):
            return f(x, y) # 调用输入的参数
        return h # 第二步开始调用
    return g # 第一步开始调用

curry2 = lambda f : lambda x : lambda y : f(x, y)

Here should be an environment diagram but none.

more clear case:

def curried_pow(x):
    def h(y):
        return pow(x, y)
    return h

>>> curried_pow(2)(3)
8

Reading(2h)¶

Chapter 1: Building Abstractions with Functions

• 1.4 Designing Functions
• 1.5 Control
• 1.6 Higher-Order Functions

Ch. 1.4¶

Functions are an essential ingredient of all programs, large and small, and serve as our primary medium to express computational processes in a programming language.

Good functions should obey following guidelines:

• only excute one job
• Don't repeat yourself(DRY)
• define generally

A function definition will often include documentation describing the function, called a docstring, which must be indented along with the function body. Docstrings are conventionally triple quoted. The first line describes the job of the function in one line. The following lines can describe arguments and clarify the behavior of the function:

When you call help with the name of a function as an argument, you see its docstring (type q to quit Python help).

例如：help(function name) 就会给出文档说明

Comment will be passed by complier but can be read by person.

# comments

As a guideline, most data values used in a function's body should be expressed as default values to named arguments, so that they are easy to inspect and can be changed by the function caller. Some values that never change, such as the fundamental constant k, can be bound in the function body or in the global frame.

Ch. 1.5¶

Instead of computing something, executing a control statement determines what the interpreter should do next.

Compound statements:
1. header
2. suite
3. clause

Practical Guidance. When indenting a suite, all lines must be indented the same amount and in the same way (use spaces, not tabs). Any variation in indentation will cause an error.

Some defines:
1. Local assignment
2. Conditional statements
3. Boolean contexts
4. Boolean values
5. Boolean operators

About boolean operators:

These procedures exploit the fact that the truth value of a logical expression can sometimes be determined without evaluating all of its subexpressions, a feature called short-circuiting.

Remark: not calculate all subexpressions

test¶

python3 -m doctest <python_source_file>

Ch. 1.6¶

To express certain general patterns as named concepts, we will need to construct functions that can accept other functions as arguments or return functions as values. Functions that manipulate functions are called higher-order functions. This section shows how higher-order functions can serve as powerful abstraction mechanisms, vastly increasing the expressive power of our language.

注：就好像泛函一样，只是这里叫高阶函数

Golden-ratio case¶

# 主要以两个函数为参数
def improve(update, close, guess = 1):
    while not close(guess): # 停机准则函数
        guess = update(guess)
    return guess

# 更新guess的函数
def golden_update(guess):
    return 1 / guess + 1

# 以guess作为输入给出判断(实际上可以合并)
def square_close_to_successor(guess):
    return approx_eq(guess * guess, guess + 1)

# 停机准则函数
def approx_eq(x, y, tolerance=1e-3):
    return abs(x - y) < tolerance

phi = improve(golden_update, square_close_to_successor)

Defining Functions III: Nested Definitions¶

相当重要的一个东西，做一个函数嵌套

Lexical scope. Locally defined functions also have access to the name bindings in the scope in which they are defined.

two key advantages of lexical scoping in Python

• The names of a local function do not interfere with names external to the function in which it is defined, because the local function name will be bound in the current local environment in which it was defined, rather than the global environment.
• A local function can access the environment of the enclosing function, because the body of the local function is evaluated in an environment that extends the evaluation environment in which it was defined.

还需要注意环境和函数的关系

Newton's Method¶

已经学了不知道多少遍了

既然讲了Newton-Raphson Algorithm也应该讲一下Fisher-scoring Algorithm吧(From Mathematical Statistic)

Currying(柯里化)¶

"Currying" 在英语中，尤其是在编程和数学领域，指的是“柯里化”。柯里化是一种将使用多个参数的函数转换为一系列使用单一参数的函数的技术。

Currying allows us to do so without writing a specific function for each number whose powers we wish to compute.

Lambda function¶

是一种简洁的函数表示方法但是由于理解的不容易不怎么使用，在Python中更倾向于使用def而不是lambda函数(为了方便别人也为了方便自己，知道这个用法应当足够，自己的程序最好还是不要用了)

Standard formal:

lambda x : f(g(x)) means "A function that takes x and returns f(g(x))"

Case:

compose1 = lambda f, g : lambda x: f(g(x))

The significance of higher-order functions is that they enable us to represent these abstractions explicitly as elements in our programming language, so that they can be handled just like other computational elements.

Function Decorators¶

相当于在原本函数的基础上增加一些新的小功能并且不更改函数名和原本调用

Question: 为什么不直接重构呢？

以下是一些可能的原因(瞎琢磨)：

• 代码复用(用一个片段一直修饰不同的函数)
• 保证原本函数的简洁
• 所谓的"开闭原则"
• 方便维护和扩展(装饰器的部分应该不是函数核心的功能，如果不用或是修改的话可以直接重构多个函数)

Lab 01(1h)¶

What Would Python Display? (WWPD)¶

Q1: WWPD: Control¶

注意：Python的函数在没有显式使用return的情况下默认返回None，print后就会得到None

例子

def how_big(x):
    if x > 10: 
        print('huge') 
    elif x > 5: 
        return 'big' 
    if x > 0: 
        print('positive') 
    else: 
        print(0)

>>> print(how_big(12))
line1 huge
line2 positive
line3 None

Q2: Debugging Quiz¶

有点搞，不知道为什么交互式做选择题比单纯做题有乐子，做题家基因觉醒了.

Write Code¶

Q3: Falling Factorial¶

唯一的问题是要把所有的doctest和题目看完，不要直接写

答案没有专门对0判断而是用了更聪明的做法(移项可知\(k>0\))

total, stop = 1, n-k  
while n > stop:  
    total, n = total*n, n-1  
return total

Q4: Divisible By k¶

相当于实现一个更完整的range函数

感觉写的不是特别好

Q5: Sum Digits¶

经典的OJ题，做法太多了

Syllabus Quiz¶

Q6: Syllabus Quiz¶

做不了

Optional Questions¶

Q7: WWPD: What If?¶

非常容易不知道和前面比难在哪

Q8: Double Eights¶

同样非常容易，OJ老题

这个参考答案节约了一些空间

def double_eights_alt(n):  
    while n:  
        if n % 10 == 8 and n // 10 % 10 == 8:  
            return True  
        n //= 10  
    return False

Disc 01(30min)¶

While and If¶

Q1: Race¶

def race(x, y):
    """The tortoise always walks x feet per minute, while the hare repeatedly
    runs y feet per minute for 5 minutes, then rests for 5 minutes. Return how
    many minutes pass until the tortoise first catches up to the hare.

    >>> race(5, 7)  # After 7 minutes, both have gone 35 steps
    7
    >>> race(2, 4) # After 10 minutes, both have gone 20 steps
    10
    """
    assert y > x and y <= 2 * x, 'the hare must be fast but not too fast'
    tortoise, hare, minutes = 0, 0, 0
    while minutes == 0 or tortoise - hare:
        tortoise += x
        if minutes % 10 < 5:
            hare += y
        minutes += 1
    return minutes

错误应该为乌龟超越兔子但二者行走距离不同，第二次追及

Wrong value：(2，3),(6, 11)

注1：直接考虑构建一个二元方程组，考虑特殊情况下运动相同距离就应该是在兔子运动时相遇，\((10+t)x=(5+t)y\)，此时只需要取整数解即可\((1\leqslant t \leqslant 5)\)，随便取一个好算的分数通分即可(注意不要循环起来也不要是整数比，两倍肯定相同，小技巧是选取互素的整数对(x, y)且gcd(x,5)=1，注意这样在第一轮就始终无法走相同距离)

注2：好像应该用试的但是没忍住分析了一下

无限运行应该是乌龟超过兔子后兔子追不上

Runs forever：(4, 5)

注3：延续上面的思路即可\((10k+t)x=(5k+t)y\)，考虑互素的情形，并且不为两倍关系直接令\(y=5\)，令\(t=5\)排除\(x=3\implies x=4\)

Q2: Fizzbuzz¶

非常简单的判断，代码参考repo

Q3: Is Prime?¶

经典素数筛，理论上有许多筛法，这里偷懒直接选用了一个最基本的数论结果

if n == 1:  
    return False  
k = 2  
while k < (n / 2):  
    # save time  
    if n % k == 0:  
        return False  
    k += 1  
return True

Q4: Unique Digits¶

完成两个函数即可，第一个只需要在第二个函数基础上写while循环

Q5: Bottles¶

pass

Q6: Double Trouble¶

HW02(30min)¶

大都比较简单，不再赘述，代码可参考仓库

评论