hw5¶
约 364 个字 206 行代码 1 张图片 预计阅读时间 4 分钟
Problem 1¶
编写一个程序,在一个文件夹中,在其中生成assignment_1.txt, assignment_2.txt,....,assignment_100.txt等100个文本文件,
文件内容为这个文件的绝对路径。
然后随机删除其中5个文件。
import os
import random
# 生成文件的函数
def generate_files(folder_path):
if not os.path.exists(folder_path):
os.makedirs(folder_path)
# 生成100个文件
for i in range(1, 101):
file_name = f"assignment_{i}.txt"
file_path = os.path.join(folder_path, file_name)
# 写入文本内容为绝对路径
with open(file_path, 'w') as file:
file.write(os.path.abspath(file_path))
# 随机删除5个文件
def delete_random_files(folder_path):
# 筛选文件名和后缀名避免误删
files = [f for f in os.listdir(folder_path) if f.startswith('assignment_') and f.endswith('.txt')]
to_delete = random.sample(files, 5)
for file in to_delete:
file_path = os.path.join(folder_path, file)
os.remove(file_path)
if __name__ == "__main__":
folder_path = "hw5_problem1_folder"
generate_files(folder_path)
delete_random_files(folder_path)
再编写另一个程序,找出缺失的5个文件,并把缺失的5个文件补齐。
import os
# 找出缺失的5个文件
def find_missing_files(folder_path):
existing_files = [f for f in os.listdir(folder_path) if f.startswith('assignment_') and f.endswith('.txt')]
# 找出未被删除的文件
existing_numbers = [int(f.split('_')[1].split('.')[0]) for f in existing_files]
all_numbers = set(range(1, 101))
missing_numbers = all_numbers - set(existing_numbers)
return missing_numbers
def recover_missing_files(folder_path, missing_numbers):
for num in missing_numbers:
file_name = f"assignment_{num}.txt"
file_path = os.path.join(folder_path, file_name)
with open(file_path, 'w') as file:
file.write(os.path.abspath(file_path))
if __name__ == "__main__":
folder_path = "hw5_problem1_folder"
missing_numbers = find_missing_files(folder_path)
# 检验操作
print(missing_numbers)
# 恢复
recover_missing_files(folder_path, missing_numbers)
# 再检验一次
missing_numbers = find_missing_files(folder_path)
print(missing_numbers)
1 2 | |
Problem 2¶
使用numpy.random.randn分别创建1010,100100和1000*1000的数据,并分别计算他们的均值和标准差。
import numpy as np
# 定义要生成的矩阵大小
sizes = [10, 100, 1000]
# 遍历不同大小
for size in sizes:
# 使用 numpy.random.randn 创建指定大小的矩阵
matrix = np.random.randn(size, size)
# 计算矩阵的均值
mean = np.mean(matrix)
# 计算矩阵的标准差
std_dev = np.std(matrix)
print(f"{size}x{size} 矩阵的均值: {mean}")
print(f"{size}x{size} 矩阵的标准差: {std_dev}")
print()
1 2 3 4 5 6 7 8 | |
Problem 3¶
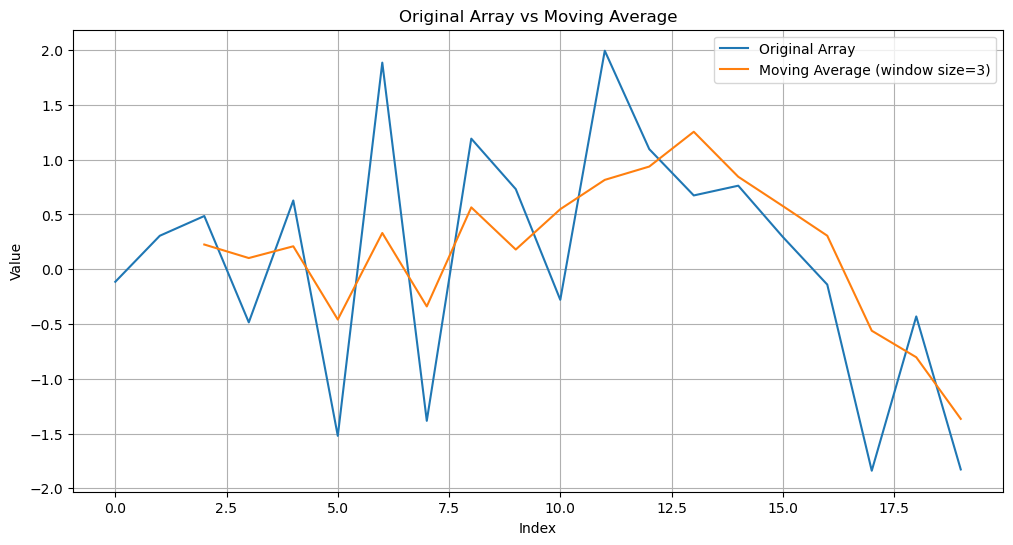
给定一个一维数组,定义函数moving_average(a,n)计算此数组的滑动平均值,a为数组,n为窗口长度。给出例子并作图显示。
import numpy as np
import matplotlib.pyplot as plt
# 定义的函数,计算滑动平均值
def moving_average(a, n):
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
# 示例数组 长度和区间长度
a = np.random.randn(20)
n = 3
moving_avg = moving_average(a, n)
# 绘图
plt.figure(figsize=(12, 6))
plt.plot(a, label = "Original Array")
plt.plot(np.arange(n - 1, len(a)), moving_avg, label = f"Moving Average (window size={n})")
plt.title("Original Array vs Moving Average")
plt.xlabel("Index")
plt.ylabel("Value")
plt.legend()
plt.grid(True)
plt.show()
Problem 4¶
对于一个任意二维数组,给定此数组中某个元素的位置(i,j)和一个长度值l,从此二维数组中提取出以此元素为中心,
维数为(2 * l + 1,2 * l + 1)的方阵。
如果越界,则使用0补齐。
import numpy as np
def extract_square_matrix(arr, i, j, l):
# 增加输入检查功能
# 检查输入数组是否为二维数组
if len(arr.shape) != 2:
raise ValueError("输入数组必须是二维数组。")
# 检查输入的 i、j、l 是否为有效整数
if not isinstance(i, int) or not isinstance(j, int) or not isinstance(l, int):
raise ValueError("i、j、l 必须是整数。")
# 获取输入数组的行数和列数
# 修正坐标
i -= 1
j -= 1
rows, cols = arr.shape
# 初始化结果矩阵,大小为 (2l+1, 2l+1),初始值全为 0
result = np.zeros((2 * l + 1, 2 * l + 1))
# 计算方阵在原数组中的起始行索引,确保不小于 0
start_row = max(0, i - l)
# 计算方阵在原数组中的结束行索引,确保不超过数组行数
end_row = min(rows, i + l + 1)
# 计算方阵在原数组中的起始列索引,确保不小于 0
start_col = max(0, j - l)
# 计算方阵在原数组中的结束列索引,确保不超过数组列数
end_col = min(cols, j + l + 1)
# 计算方阵在结果矩阵中的起始行偏移量
offset_row_start = start_row - (i - l)
# 计算方阵在结果矩阵中的结束行偏移量
offset_row_end = offset_row_start + (end_row - start_row)
# 计算方阵在结果矩阵中的起始列偏移量
offset_col_start = start_col - (j - l)
# 计算方阵在结果矩阵中的结束列偏移量
offset_col_end = offset_col_start + (end_col - start_col)
# 将原数组中提取的方阵赋值给结果矩阵的相应位置
result[offset_row_start:offset_row_end, offset_col_start:offset_col_end] = arr[start_row:end_row, start_col:end_col]
return result
# 多测试点
arr = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]])
i, j = 2, 3
l = 1
submatrix = extract_square_matrix(arr, i, j, l)
print(submatrix)
print("\n")
i, j = 2, 1
l = 3
submatrix = extract_square_matrix(arr, i, j, l)
print(submatrix)
print("\n")
i, j = 2, 1
l = 2
submatrix = extract_square_matrix(arr, i, j, l)
print(submatrix)
print("\n")
i, j = 2, 3
l = 4
submatrix = extract_square_matrix(arr, i, j, l)
print(submatrix)
1 2 3 | |
[[ 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 1. 2. 3. 4.]
[ 0. 0. 0. 5. 6. 7. 8.]
[ 0. 0. 0. 9. 10. 11. 12.]
[ 0. 0. 0. 13. 14. 15. 16.]
[ 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 1. 2. 3.]
[ 0. 0. 5. 6. 7.]
[ 0. 0. 9. 10. 11.]
[ 0. 0. 13. 14. 15.]]
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 1. 2. 3. 4. 0. 0. 0.]
[ 0. 0. 5. 6. 7. 8. 0. 0. 0.]
[ 0. 0. 9. 10. 11. 12. 0. 0. 0.]
[ 0. 0. 13. 14. 15. 16. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
Problem 5¶
设二次函数 p(x)=ax^2+bx+c过点(x_i,y_i) for i=1, 2, 3. 求a,b,c的值。
例如过这三个点(-1,1),(0,-1),(2,7),则可以得到一个线性方程组,使用numpy.linalg中solve函数解方程即可。
import numpy as np
# 利用基本的线性代数知识求解
def find_coefficients(points):
# 构建线性方程组的系数矩阵 A 和常数矩阵 B
A = []
B = []
for x, y in points:
A.append([x**2, x, 1])
B.append(y)
A = np.array(A)
B = np.array(B)
# 求解线性方程组
try:
coefficients = np.linalg.solve(A, B)
return coefficients
except np.linalg.LinAlgError:
print("线性方程组无解或有无穷多解。")
return None
# 示例点
points = [(-1, 1), (0, -1), (2, 7)]
coefficients = find_coefficients(points)
if coefficients is not None:
a, b, c = coefficients
print(f"二次函数系数: a = {a}, b = {b}, c = {c}")
1 | |